Probability Recap

These are my summary notes that I brought to the open-note exams when I took ECE 534: Random Processes at UIUC back in Spring 2011. This part covers Sections 1.1 - 1.6 from Prof. Bruce Hajek’s lecture notes.

1.1 The Axioms of Probability Theory

Probability Space \((\Omega, F, P)\)
\(\Omega\) : sample space
\(F\) : set of events \(=\) collection of subsets of \(\Omega\)
\(P\) : probability measure on \(F\)

\(\sigma\)-algebra: Satisfying the axioms below
[A.1] \(\Omega \in F\)
[A.2] If \(A \in F\) then \(A^\mathsf{c} \in F\)
[A.3] If \(A, B \in F\) then \(A \cup B \in F\)

Probability Measure: satisfying the axioms below
[P.1] \(P[A] \ge 0 \ \forall A \in F\)
[P.2] \(A, B \in F\) and \(A, B\) mutually exclusive \(\Rightarrow P[A \cup B] = P[A] + P[B]\)
[P.3] \(P[ \Omega ] = 1\)

Borel \(\sigma\)-algebra for \(\mathbb{R}\): smallest \(\sigma\)-algebra containing the open subsets of \(\mathbb{R}\)

Some properties for any subsets \(A, B, C, \in F\)
[1] If \(A \subset B\) then \(P[A] \le P[B]\)
[2] \(P[A \cup B] = P[A] + P[B] - P[AB]\)
[3] \(P[A \cup B \cup C] = P[A] + P[B] + P[C] - P[AB] - P[AC] - P[BC] + P[ABC]\)
[4] \(P[A] + P[A^\mathsf{c}] = 1\)
[5] \(P[ \varnothing ] = 0\)

Continuity of Probability
[a] If \(B_1 \subset B_2 \subset ...\) then \(\lim_{j \rightarrow \infty} P[B_j] = P[\bigcup_{i = 1}^{\infty} B_i]\)
[b] If \(B_1 \supset B_2 \supset ...\) then \(\lim_{j \rightarrow \infty} P[B_j] = P[\bigcap_{i = 1}^{\infty} B_i]\)

1.2 Independence and Conditional Probability

\(A_1, A_2, ..., A_k\) are independent if
\(P[A_{i1}, A_{i2}, ..., A_{ij}] = P[A_{i1}] ... P[A_{ij}]\) with \(j \ge 1\) and \(1 \le i_1 \le i_2 \le ... \le i_j \le k\)

\(A, B, C\) are independent if
[1] \(P[AB] = P[A]P[B]\)
[2] \(P[AC] = P[A]P[C]\)
[3] \(P[BC] = P[B]P[C]\)
[4] \(P[ABC] = P[A]P[B]P[C]\)
[1]-[3] are conditions for pairwise independence. In general, there are \(\binom{n}{2} = \frac{n(n-1)}{2}\) conditions.

Independent: \(\mathbb{E}[XY] = \mathbb{E}X\mathbb{E}Y \Rightarrow\)

Uncorrelated: \(Cov(X,Y) = \mathbb{E}[XY] - \mathbb{E}X\mathbb{E}Y = 0\)

Conditional Probability: (\(P[B] \neq 0\))
\(P[A|B] = \frac{P[AB]}{P[B]}\) (not defined if \(P[B] = 0\))

Bayes’ Formula: (\(P[A] \neq 0\))
\(P[B|A] = \frac{P[AB]}{P[A]} = \frac{P[A|B]P[B]}{P[A]}\)
\(P[E_i|A] = \frac{P[A|E_i]P[E_i]}{P[A|E_1]P[E_1] + ... + P[A|E_k]P[E_k ]}\)

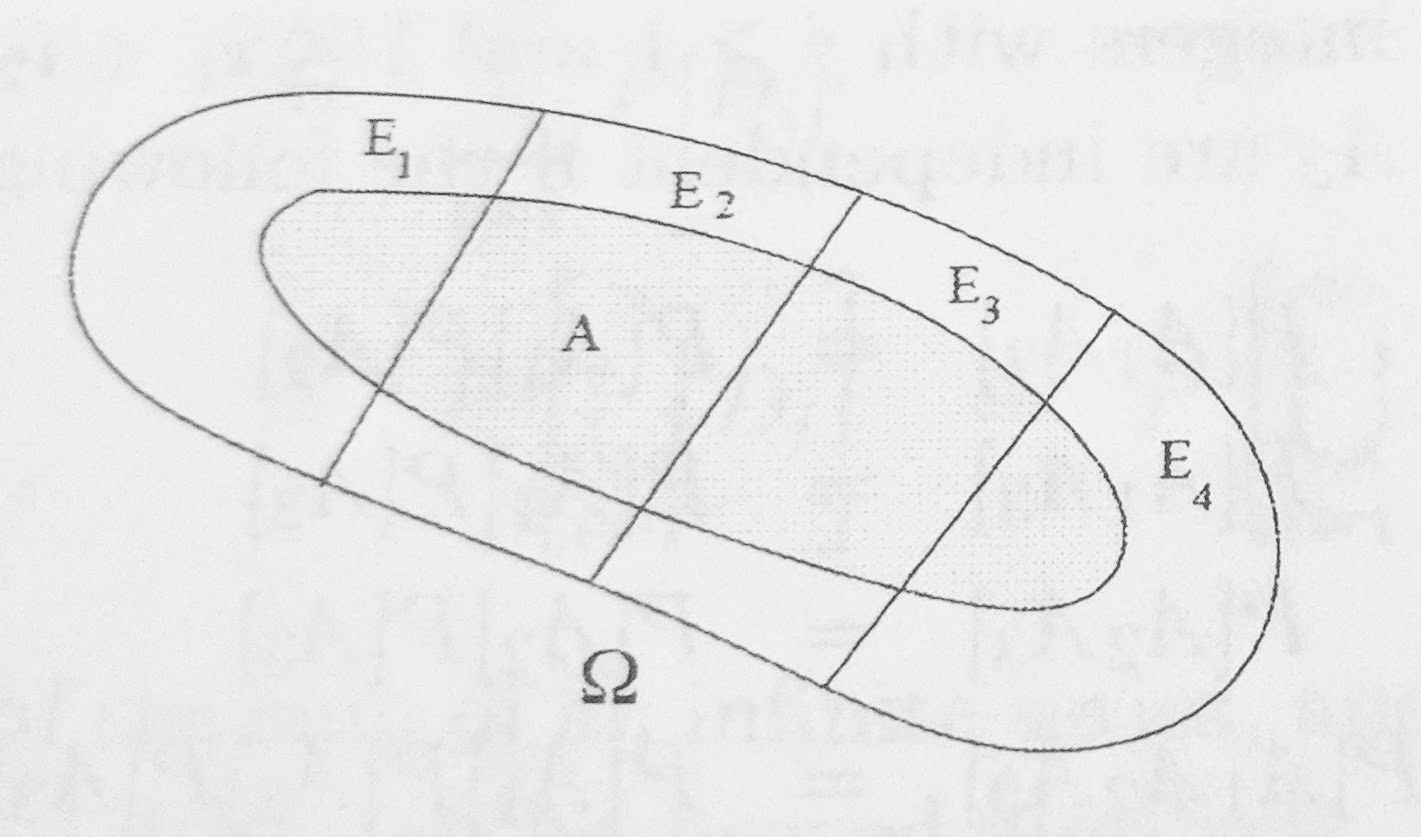
The event {\(A_n\) infinitely often} is the set of \(\omega \in \Omega\) s.t. \(\omega \in A_n\) for infinitely many values of \(n\)

Borel-Cantelli Lemma:
Let \(A_n\) : \(n \ge 1\) be a sequence of events and let \(P_n = P[A_n]\)
[a] If \(\sum_{n=1}^{\infty} P_n < \infty\) then \(P\){\(A_n\) infinitely often} \(= 0\)
[b] If \(\sum_{n=1}^{\infty} P_n = \infty\) and \(A_1, A_2, ...\) are mutually independent, then \(P\){\(A_n\) infinitely often} \(= 1\)

1.3 Random Variables and Their Distribution

Random Variable
Given a probability space \((\Omega, F, P)\), a real-valued random variable is an \(F\)-measurable function \(X: \Omega \rightarrow \mathbb{R}\) \(\omega \in \Omega \Rightarrow X(\omega) \in \mathbb{R}\)

A binary random variable is an \(F\)-measurable function \(X: \Omega \rightarrow {0, 1}\)

Cumulative Distribution Function (CDF) of a random variable
\(X: \Omega \rightarrow \mathbb{R}\) is defined as
\(\forall x \in \mathbb{R}\), \(F(x) = P{\omega \in \Omega : X(\omega) \le x} = P[X \le x]\)

Properties of the CDF
[F.1] \(F\) is nondecreasing
[F.2] \(\lim_{x \rightarrow +\infty} F(x) = 1\) and \(\lim_{x \rightarrow -\infty} F(x) = 0\)
[F.3] \(F\) is right continuous
(F.4) \(0 \le F(x) \le 1 \ \forall x \in \mathbb{R}\)
\(P\{X < c\} = \lim_{i \rightarrow \infty} P\{X \le c_i\} = \lim_{i \rightarrow \infty} F_x(c_i) = F_x(c-)\)
\(P\{X = c\} = F_x(c) - F_x(c-) = \Delta F_x(c)\)
\(X\) is a random variable on \((\Omega, F, P) \Leftrightarrow X\) has a CDF

A random variable \(X\) is discrete \(\Leftrightarrow \exists\) countable set \(\{ x_i, i \in I \}\) s.t. \(P\{ \omega \in \Omega, X(\omega)=x\): for some \(i \}\)

A random variable \(X\) is continuous \(\Leftrightarrow \exists\) function \(f(x)\) s.t. the CDF \(F(X) = \int_{-\infty}^{x} f(y)dy\)
where \(f(x)\) is called the probability density function (PDF) of \(x\)
\(\Rightarrow f(x) = F'(x)\)
The probability mass function (PMF) of \(x\) is \(P(x_i) := F(x_i) - F(x_i-)\)

A mixed random variable is anything else (not countable/differentiable)

1.4 Functions of a Random Variable

Compute \(Y = g(X)\)
[1] Examine the range of \(X, Y\), sketch \(g\)
[2] Find the CDF of Y, \(F_Y(c) = P(Y \le c) = P(g(x) \le c)\) for \(\{ X \in A \}\) depending on \(c\)
[3.1] If \(F_Y\) has a piecewise continuous derivative, and \(f_Y\) is desired, then differentiate \(F_Y\)
[3.2] If \(X\) is discrete, \(P_Y(y) = P \{g(x)=y \} = \sum_{x:g(x)=y}P_x(x)\)

1.5 Expectation of a Random Variable

Expectation of a random variable \(X\) over \((\Omega, F, P)\)

• Discrete random variable
  \(P[X = x:\) for some \(i \in I] = 1\)
  \(p_i = P[X=x_i], i \in I\)
  [1] \(\mathbb{E}[X] := \sum_{i \in I} x_i p_i =  \sum_{i \in I} x_i P(E_i)  = \sum_{i \in I} x_i \sum_{\omega \in E_i} P(\omega) = \sum_{i \in I} \sum_{\omega \in E_i} x_i P(\omega)\)
  [2] \(\mathbb{E}[X] = \sum_{\omega \in \Omega} X(\omega)P(\omega)\)/
  
• Continuous random variable \(X\) with CDF \(F(x)\) and PDF \(f(x)\)
  [1] \(\mathbb{E}[X] = \int_{-\infty}^{\infty} xp(x)dx\)
  [2] \(\mathbb{E}[X] = \int_{-\infty}^{\infty} xF(dx) = \int_{-\infty}^{\infty} xdF_X(x) = \int_{-\infty}^{\infty} xP(E(dx))\)
  [3] \(\mathbb{E}[X] := \int_{\Omega} X(\omega)P(d\omega)\)
  

Transformation \(Y=g(X)\)
\(\begin{array}{ccl} \mathbb{E}[Y] & = &  \mathbb{E}[g(X)] \\ & = & \sum_{i \in I} g(x_i)p_i \\ & = & \sum_{x} g(x)p_X(x) \\ & = & \sum_{y}yp_Y(y) \\ & = & \sum_{\omega \in \Omega} Y(\omega)P(\omega) \\ & = & \sum_{\omega \in \Omega}g(X(\omega)) \end{array}\)

Properties of Expectation
[E.1] \(\mathbb{E}[cX] = c\mathbb{E}[X]\), \(\mathbb{E}[X+Y] = \mathbb{E}[X] + \mathbb{E}[Y]\)
[E.2] \(P\{X \ge Y\} = 1\) and \(\mathbb{E}[X]\) and \(\mathbb{E}[Y]\) will be defined \(\Rightarrow \mathbb{E}[X] \ge \mathbb{E}[Y]\)
[E.3] \(\mathbb{E}[X] = \int_{-\infty}^{\infty} x f_X(x)dx\) (PDF)
[E.4] \(\mathbb{E}[X] = \sum_{x>0} x p_X(x) + \sum_{x<0} x p_X(x)\) (PMF)
[E.5] \(\mathbb{E}[g(X)] = \int_{-\infty}{\infty} g(x) f_X(x) dx\)

Wald’s Equation: \(\mathbb{E}[\sum_{i=1}^{N}X_i] = \mathbb{E}[N]\mathbb{E}[X]\)

Variance
\(\begin{array}{ccl} Var[X] & := & \mathbb{E}[(X - \mathbb{E}X)^2] \\ & = & \mathbb{E}[X^2 -2X\mathbb{E}X + \mathbb{E}^2[X]] \\ & = & \mathbb{E}[X^2] - \mathbb{E}[2X \mathbb{E}X] + \mathbb{E}[\mathbb{E}^2[X]] \\ & = & \mathbb{E}[X^2] - 2\mathbb{E}^2[X] + \mathbb{E}[X] \\ & = & \mathbb{E}[X^2] - \mathbb{E}^2[X] \end{array}\)

Markov’s Inequality: \(P\{Y \ge C\} \le \frac{\mathbb{E}[Y]}{C} (\le 1)\) for nonnegative \(Y (Y \ge 0)\)

Chebyshev’s Inequality: \(P\{\vert X - \mu \vert \ge d\} \le \frac{\sigma^2}{d^2}\)

Characteristic function associated with PDF:
\(\Phi_x(u) := \int_{-\infty}^{\infty} e^{jux}f(x)dx, j=\sqrt{-1}, u \in \mathbb{R}\)
\(\frac{d\Phi_x}{du} = \Phi_x'(u) = \int_{-\infty}^{\infty}jx \cdot e^{jux} f(x)dx\)
\(\Phi_x'(0) = \int_{-\infty}^{\infty} xf(x)dx\)
\(\mathbb{E}[X] = \frac{\Phi_x'(0)}{j}\)
k^th moment: \(\mathbb{E}[X^k] = \frac{\Phi_x^{(k)}(0)}{j^k} \ \forall k = 1, 2, ...\)

1.6 Frequently Used Distributions

Bernoulli: \(Be(p), 0 \le p \le 1\)
pmf: \(p(i) = \begin{cases} p & \text{ if } \ i=1\\ 1-p & \text{ if } \ i=0\\ 0 & \text{ else } \ \end{cases}\)
z-transform: \(1-p+pz\), where \(z = e^{ju}\)
mean: \(p\)
variance: \(p - p^2 = p(1-p)\)

Binomial: \(Bi(n,p), n \ge 1, 0 \le p \le 1\)
pmf: \(p(i) = \binom{n}{i}p^i(1-p)^{n-i}, 0 \le i \le n\)
z-transform: \((1-p+pz)^n\)
mean: \(np\)
variance: \(np(1-p)\)

Poisson: \(Poi(\lambda), \lambda \ge 0\)
pmf: \(p(i)=\frac{\lambda^i e^{-\lambda}}{i!}, i \ge 0\)
z-transform: \(\exp(\lambda(z-1))\)
mean: \(\mathbb{E}[X] = \sum_{i=0}^{\infty}i P(X=i) = \sum_{i=0}^{\infty}i \frac{e^{-\lambda}\lambda^i}{i!} = \lambda e^{-\lambda} \sum_{i=0}^{\infty} \frac{\lambda^{i-1}}{(i-1)!} = \lambda e^{-\lambda} \sum_{i=0}^{\infty} \frac{\lambda^i}{i!} = \lambda e^{-\lambda}e^{\lambda} = \lambda\)
variance: \((\lambda + \lambda^2) - \lambda^2 = \lambda\)
\(Poi(\lambda)\) is the limit of \(Bi(n,p)\) as \(n \rightarrow +\infty, p \rightarrow 0\) in such a way that \(np \rightarrow \lambda\)

Geometric: \(Geo(p), 0 \lt p \le 1\)
pmf: \(p(i) = (1-p)^{i-1}p, i \ge 1\)
z-transform: \(\frac{pz}{1-z+pz}\)
mean: \(\mathbb{E}[X] = \sum_{x=1}^{\infty}xp(1-p)^{x-1} = \frac{p}{1-p}\sum_{x=1}^{\infty}x(1-p)^x = \frac{p}{1-p}\frac{1-p}{[1-(1-p)]^2} = \frac{1}{p}\)
variance: \(\mathbb{E}[X^2] = \sum_{x=1}^{\infty}x^2p(1-p)^{x-1} = \frac{p}{1-p} \sum_{x=1}^{\infty}x^2(1-p)^x = \frac{2-p}{p^2}\)
\(Var[X] = \frac{1-p}{p^2}\)
Memoryless:
\(P\{X>i\}=(1-p)^i\) for integers \(i \ge 1\)
\(P\{X>i+j|X>i\} = P\{X>j\}\) for \(i,j \ge 1\)

Gaussian: \(N(\mu, \sigma^2), \mu \in \mathbb{R}, \sigma \ge 0\)
pdf (if \(\sigma^2 > 0\)): \(f(x) = \frac{1}{\sqrt{2\pi \sigma^2}} \exp(-\frac{(x-\mu)^2}{2\sigma^2})\)
pmf (if \(\sigma^2 = 0\)): \(p(x) = \begin{cases} 1 & \text {if} \ x = \mu\\ 0 & \text {else} \end{cases}\) characteristic function: \(\exp(ju\mu-\frac{u^2\sigma^2}{2})\)
mean: \(\mu\)
variance: \(\sigma^2\)
\(\mathbb{E}[X^2] = \mu^2 + \sigma^2\)
mgf (moment-generating function): \(\exp(\mu t+\frac{1}{2}\sigma^2t^2)\)
\(\Phi\): CDF of a \(N(0,1)\) random variable
\(Q(c) = 1 - \Phi(c) = \int_{c}^{\infty}\frac{1}{\sqrt{2\pi}}e^{-\frac{x^2}{2}}dx\)
\(P\{X \ge c\} = Q(\frac{c-\mu}{\sigma})\)

Central Limit Theorem:
If \(X_1, X_2,...\) are i.i.d. with mean \(\mu\) and nonzero variance \(\sigma^2\), then for any constant \(c\)
\(\lim_{n \rightarrow \infty} P \{\frac{X_1+...+X_n-n\mu}{n\sigma^2} \le c\} = \Phi(c)\)

Exponential: \(Exp(\lambda), \lambda > 0\)
pdf: \(f(x) = \lambda e^{-\lambda x}, x \ge 0\)
cdf: \(F(x) = 1 - e^{-\lambda x}, x \ge 0\)
characteristic function: \(\frac{\lambda}{\lambda - ju}\)
mean: \(\mathbb{E}[X] = \int_{-\infty}^{\infty}x(\lambda e^{-\lambda x})dx = \left[ -x e^{-\lambda x} \right]_{0}^{\infty} + \int_{0}^{\infty} e^{-\lambda x} dx = 0 - \left[ \frac{1}{\lambda} e^{-\lambda x} \right]_{0}^{\infty} = \frac{1}{\lambda}\)
variance: \(\mathbb{E}[X^2] = \int_0^{\infty}x^2 (\lambda e^{-\lambda x}) dx = \frac{2}{\lambda^2}\)
\(Var[X] = \frac{1}{\lambda^2}\)
Memoryless:
\(P\{X \ge t\} = e^{-\lambda t}\) for \(t \ge 0\)
\(P\{X \ge s + t | X \ge s\} = P\{ X \ge t\}, s,t \ge 0\)

Uniform: \(U(a,b), -\infty \lt a \lt b \lt \infty\)
pdf: \(f(x) = \begin{cases} \frac{1}{b-a} & \text{ if } \ a \le x \le b\\ 0 & \text{ else } \ \end{cases}\) characteristic function: \(\frac{e^{jub} - e^{jua}}{ju(b-a)}\)
mean: \(\frac{a+b}{2}\)
variance: \(\frac{(b-a)^2}{12}\)

Gamma: \(Gamma(n, \alpha), n, \alpha > 0, n \in \mathbb{R}\)
pdf: \(f(x) = \frac{\alpha^n x^{n-1} e^{-\alpha x}}{\Gamma(n)}, x \ge 0\)
where \(\Gamma(n) = \int_{0}^{\infty}s^{n-1}e^{-s}ds\)
characteristic function: \(\left( \frac{\alpha}{a-ju}\right) ^n\)
mean: \(\frac{n}{\alpha}\)
variance: \(\frac{n}{\alpha^2}\)
If \(n \in \mathbb{N}^+\) then \(\Gamma(n) = (n-1)!\)
\(Gamma(n,\alpha)\) = sum of n i.i.d. \(Exp(\alpha)\)

Rayleigh: \(Raleigh(\sigma^2), \sigma^2 > 0\)
pdf: \(f(r) = \frac{r}{\sigma^2}\exp(-\frac{r^2}{2\sigma^2}), r > 0\)
cdf: \(1-\exp(-\frac{r^2}{2\sigma^2})\)
mean: \(\sigma \sqrt{\frac{\pi}{2}}\)
variance: \(\sigma^2(2 - \frac{\pi}{2})\)
If \(X, Y \sim N(0, \sigma^2)\) then \(\sqrt{X^2 + Y^2} \sim Rayleigh(\sigma^2)\)

Multinomial
pmf: \(p(x_1, x_2, ..., x_r) = P(X_1 = x_1, X_2 = x_2, ..., X_r = x_r) = \frac{n!}{x_1!x_2!...x_r!}p_1^{x_1}p_2^{x_2}...p_r^{x_r}\)
marginalize over \(x_1, x_2, x_3 \Rightarrow\) multinomial with \(n\) and \(p_1, p_2, p_3, 1-p_1-p_2-p_3\)